Data Structures & Algorithms Learning Plaza - Array

This series is dedicated to documenting my insights and notes as I study Data Structures and Algorithms. I’ll primarily be using Python to solve problems, and my LeetCode solutions will be stored in my Learning Plaza repo. For my LeetCode practicing sequence, I’m following the guidance from 代码随想录 (content in Chinese), while also refer to Labuladong Algo Notes. As the first post in this series, this article will focus on Array.

P.S. Today marks the 龙抬头 (“Dragon raising its head”) Festival in the Chinese Lunar Year 2025, and it’s also the first day of March. I’m hoping to kick off this year’s learning adventure with a fresh new start! Let’s do this!

Fundamentals of Array

Excerpt and translate from 代码随想录.

How Arrays are Stored in Memory

Arrays are data structures that store elements of the same type in a contiguous block of memory.

Some friends might wonder: can’t Python’s list store different data types? Indeed, Python offers multiple array-like data structures, each with distinct characteristics:

• The built-in list type, which is dynamic and can hold elements of varying types.
• The array type from the array module, which restricts elements to a single type.
• The ndarray from the numpy library, optimized for numerical computations and capable of supporting multi-dimensional arrays.

>>> my_lst = [1,2,3]    # list
>>> import array    # built-in library
>>> my_arr = array.array('i', [1, 2, 3])    # array
>>> import numpy as np
>>> np_arr = np.array([1, 2, 3])    # numpy array
>>> print(type(my_lst))
<class 'list'>
>>> print(type(my_arr))
<class 'array.array'>
>>> print(type(np_arr))
<class 'numpy.ndarray'>    # ndarrary -> N-dimensional array

Characteristics of Arrays

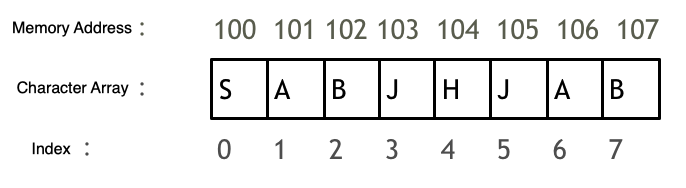
Array’s contiguous allocation enables efficient access to any element using its index.

Here’s an example of a character array, as shown in the figure:

Two important points:

• Array indices always start at 0.
• The memory addresses of array elements are contiguous.

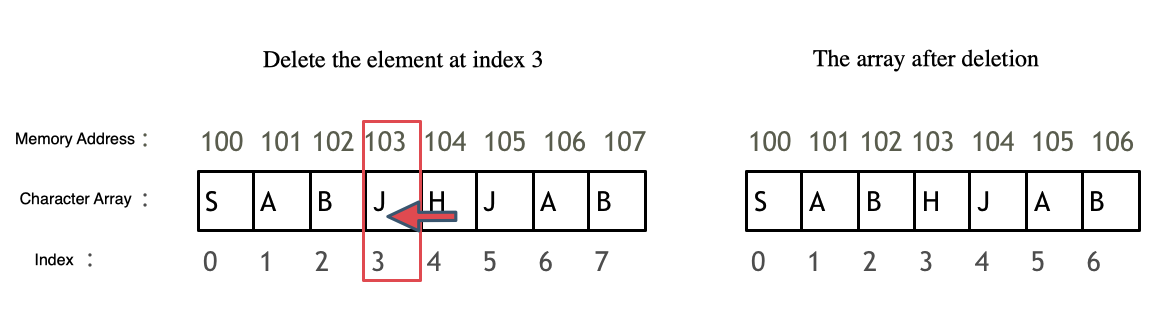
This contiguous allocation makes operations like insertion and deletion more expensive due to the need to shift elements.

For example, when deleting the element at index 3, all elements after that index must be shifted, as shown in the figure:

Array elements can’t really be deleted, they can only be overwritten.

This doesn’t mean that arrays don’t support deletion operations, but rather that deletion is implemented by overwriting the data.

Binary Search

Since binary search is both classic and crucial, and it involves numerous details, I have dedicated a separate post to explain it in depth and covers some related problems:

• 704: classic binary search
• 35: demonstrates the return value of binary search
• 34: find left and right boundaries
• 69 and 367

For more details, please visit: Data Structures & Algorithms Learning Plaza - Binary Search.

Remove Element

LeetCode link: 27

Description

Given an integer array nums and an integer val, remove all occurrences of val in nums in-place. The order of the elements may be changed. Then return the number of elements in nums which are not equal to val.

Consider the number of elements in nums which are not equal to val be k, to get accepted, you need to do the following things:

• Change the array nums such that the first k elements of nums contain the elements which are not equal to val. The remaining elements of nums are not important as well as the size of nums.
• Return k.

Custom Judge:

The judge will test your solution with the following code:

int[] nums = […]; // Input array
int val = …; // Value to remove
int[] expectedNums = […]; // The expected answer with correct length.
           // It is sorted with no values equaling val.

int k = removeElement(nums, val); // Calls your implementation

assert k == expectedNums.length;
sort(nums, 0, k); // Sort the first k elements of nums
for (int i = 0; i < actualLength; i++) {
 assert nums[i] == expectedNums[i];
}

If all assertions pass, then your solution will be accepted.

Example 1:

Input: nums = [3,2,2,3], val = 3
Output: 2, nums = [2,2,_,_]
Explanation: Your function should return k = 2, with the first two elements of nums being 2.
It does not matter what you leave beyond the returned k (hence they are underscores).

Example 2:

Input: nums = [0,1,2,2,3,0,4,2], val = 2
Output: 5, nums = [0,1,4,0,3,_,_,_]
Explanation: Your function should return k = 5, with the first five elements of nums containing 0, 0, 1, 3, and 4.
Note that the five elements can be returned in any order.
It does not matter what you leave beyond the returned k (hence they are underscores).

Constraints:

• 0 <= nums.length <= 100
• 0 <= nums[i] <= 50
• 0 <= val <= 100

Problem-solving approach

This problem officially marks the beginning of our exploration into the two-pointer approach. As discussed earlier in the Characteristics of Arrays, we cannot simply delete elements from an array in Python. Deleting an element is an O(n) operation because it requires shifting all subsequent elements to fill the gap. And the problem specifies that we only need to return the new length k of the array, ensuring that the first k elements of nums contain the elements not equal to val. This means we can cleverly overwrite the first k elements without relying on costly deletions.

This is where the two-pointer proves its value. We can set two pointers: a fast pointer and a slow pointer. The fast pointer iterates through the entire array, checking each element in turn. If the element at the fast pointer is not equal to val, we copy that element to overwrite the position of the slow pointer and increment the slow pointer. By doing so, we efficiently construct the first k elements of the array to meet the problem’s requirements.

Solution

class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        slow, fast = 0, 0

        while fast < len(nums):
            if nums[fast] != val:
                nums[slow] = nums[fast]
                slow += 1
            fast += 1
        return slow

Relevant Problem Recommendations

Remove Duplicates from Sorted Array

LeetCode link: 26

This problem closely resembles Problem 27’s approach, with the key difference lying in the condition when the slow pointer moves forward. Since the array is provided in non-decreasing order, all duplicate elements are guaranteed to be adjacent. This allows us to use the fast pointer to compare each element with its previous position. If they are equal, the element is a duplicate; if they differ, we overwrite the current position of the slow pointer with the fast pointer’s element and then increment the slow pointer.

However, there’s an important detail to consider: because we’re comparing each element with the previous one, the fast pointer’s starting position should be set to index 1 rather than 0 to avoid an index-out-of-bounds error. As a result, we begin our iteration from the second element of the array. So we also need to overwrite the slow pointer start at index 1.

Typically, the first step is to check whether the given array is empty. But the problem constraints specify that the array length is always greater than one, so we can safely ignore this scenario. That said, it’s always good practice to consider boundary conditions when designing algorithms, as they can help identify potential edge cases.

class Solution:
    def removeDuplicates(self, nums: List[int]) -> int:
        # if not nums:
        #     return 0

        fast, slow = 1, 1

        while fast < len(nums):
            if nums[fast] != nums[fast-1]:
                nums[slow] = nums[fast]
                slow += 1
            fast += 1
        return slow

Move Zeroes

LeetCode link: 283

This problem is more similar to Problem 27. The key point to note is that the problem requires moving all zeros to the end of the array while maintaining the order of non-zero elements. Therefore, after overwriting the non-zero elements, the slow pointer should continue moving forward to overwrite the remaining elements with zeros.

class Solution:
    def moveZeroes(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        slow, fast = 0, 0

        while fast < len(nums):
            if nums[fast] != 0:
                nums[slow] = nums[fast]
                slow += 1
            fast += 1

        while slow < len(nums):
            nums[slow] = 0
            slow += 1

Backspace String Compare

LeetCode link: 844

Description

Given two strings s and t, return true if they are equal when both are typed into empty text editors. '#' means a backspace character.

Note that after backspacing an empty text, the text will continue empty.

Example 1:

Input: s = "ab#c", t = "ad#c"
Output: true
Explanation: Both s and t become "ac".

Example 2:

Input: s = "ab##", t = "c#d#"
Output: true
Explanation: Both s and t become "".

Example 3:

Input: s = "a#c", t = "b"
Output: false
Explanation: s becomes "c" while t becomes "b".

Constraints:

• 1 <= s.length, t.length <= 200
• s and t only contain lowercase letters and '#' characters.

Follow up: Can you solve it in O(n) time and O(1) space?

Problem-solving approach

For this problem, the most intuitive approach is still the two-pointer. We can set up a fast pointer and a slow pointer that traverse the string simultaneously. Whenever the fast pointer points to #, the slow pointer moves back 1.

However, in Python, strings are immutable objects, meaning we cannot directly overwrite the character at the slow pointer’s position in place. So we need to create an array of the same length as the string, modify the array accordingly, and then compare the elements up to the position where the slow pointer stops in both arrays.

So in Python, this approach does not meet the Follow up requirement. Creating an array requires O(n) space. To satisfy the O(1) space requirement, we must find a way to compare the two strings directly without using additional space. A practical solution is to traverse the strings from the end toward the beginning. This allows us to simulate the backspacing operation effectively, identifying the next valid character that hasn’t been backspaced, and then comparing these valid characters one by one.

Finding the Next Valid Character

Let’s first consider how to identify the next valid character. Since # characters can appear randomly and even consecutively, we can use a counter to track the number of # characters. This counter helps us skip over the appropriate number of characters that should be backspaced. For better code reusability, we can encapsulate this logic into a function.

Comparing the Characters

The next step is to determine how to compare the characters. For two strings to be considered identical after backspacing, both pointers must fully traverse their respective strings. Therefore, in the loop condition, we should use or to check whether either pointer has not yet reached the beginning of its string. The strings are different if the valid characters at the current positions do not match, or if one pointer reaches the beginning while the other does not.

Solution

# two-pointer
class Solution:
    def backspaceCompare(self, s: str, t: str) -> bool:
        if self.resLst(s) == self.resLst(t):
            return True
        return False

    def resLst(self, s: str) -> list:
        s_lst = list(s)

        slow, fast = 0, 0
        while fast < len(s_lst):
            if s_lst[fast] == '#' and slow > 0:
                slow -= 1
            elif s_lst[fast] != '#':
                s_lst[slow] = s_lst[fast]
                slow += 1
            fast += 1
        return s_lst[:slow]

# python O(1) space complexity
class Solution:
    def backspaceCompare(self, s: str, t: str) -> bool:
        s_ptr, t_ptr = len(s) - 1, len(t) - 1

        while s_ptr >= 0 or t_ptr >= 0:
            s_ptr = self.nextValidIndex(s, s_ptr)
            t_ptr = self.nextValidIndex(t, t_ptr)

            if s_ptr >=0 and t_ptr >= 0:
                if s[s_ptr] != t[t_ptr]:
                    return False

            if s_ptr < 0 and t_ptr >= 0:
                return False
            elif s_ptr >= 0 and t_ptr < 0:
                return False

            s_ptr -= 1
            t_ptr -= 1

        return True

    def nextValidIndex(self, s, s_ptr):
        back_cnt = 0
        while s_ptr >= 0:
            if s[s_ptr] == '#':
                back_cnt += 1
                s_ptr -= 1
            elif back_cnt > 0:
                back_cnt -= 1
                s_ptr -= 1
            else:
                return s_ptr
        return -1

Squares of a Sorted Array

LeetCode link: 977

Description

Given an integer array nums sorted in non-decreasing order, return an array of the squares of each number sorted in non-decreasing order.

Example 1:

Input: nums = [-4,-1,0,3,10]
Output: [0,1,9,16,100]
Explanation: After squaring, the array becomes [16,1,0,9,100].
After sorting, it becomes [0,1,9,16,100].

Example 2:

Input: nums = [-7,-3,2,3,11]
Output: [4,9,9,49,121]

Constraints:

• 1 <= nums.length <= 10^4
• -10^4 <= nums[i] <= 10^4
• nums is sorted in non-decreasing order.

Follow up: Squaring each element and sorting the new array is very trivial, could you find an O(n) solution using a different approach?

Problem-solving approach

When solving this problem, we can continue to use the two-pointer approach, but there’s a not-so-obvious trick: how to insert the squared values in the correct order. Given that the input array is sorted in non-decreasing order, we can infer that the largest squared value will either come from the smallest negative number or the largest positive number. The squared values form a valley shape, where the largest values are at the two ends and the smallest is in the middle.

By using two pointers, we can progressively move toward the center, always selecting the larger squared value. So that we can insert values one by one and reverse the array at the end. But we can construct the result more straightforward, inserting the values from the back of a pre-allocated array, thereby achieving the final result directly.

Solution

class Solution:
    def sortedSquares(self, nums: List[int]) -> List[int]:
        res = [0 for _ in range(len(nums))]

        left = 0
        right = len(nums) - 1
        res_ptr = right

        while left <= right:
            if nums[left]**2 >= nums[right]**2:
                res[res_ptr] = nums[left]**2
                left += 1
            else:
                res[res_ptr] = nums[right]**2
                right -= 1
            res_ptr -= 1

        return res

Minimum Size Subarray Sum

LeetCode link: 209

Description

Given an array of positive integers nums and a positive integer target, return the minimal length of a subarray whose sum is greater than or equal to target. If there is no such subarray, return 0 instead.

Example 1:

Input: target = 7, nums = [2,3,1,2,4,3]
Output: 2
Explanation: The subarray [4,3] has the minimal length under the problem constraint.

Example 2:

Input: target = 4, nums = [1,4,4]
Output: 1

Example 3:

Input: target = 11, nums = [1,1,1,1,1,1,1,1]
Output: 0

Constraints:

• 1 <= target <= 10^9
• 1 <= nums.length <= 10^5
• 1 <= nums[i] <= 10^4

Problem-solving approach

This problem is a classic sliding window algorithm, which is essentially a variation of the two-pointer approach. We need to maintain a window that meets the problem’s requirements and dynamically adjusting the left and right boundaries, which also means moving the two pointers.

In this problem, we aim to find the minimum length subarray whose sub_sum >= target. To achieve this, we first expand the right boundary until the sum within the window meets sub_sum >= target. At this point, we’ve found a potential solution. But we need to note that, since neither pointer has moved forward yet, the length of the subarray is calculated as right - left + 1.

Next, we continuously move the left boundary to shrink the subarray while updating the minimum length, until the sum within the window falls below the target. Now we can move the right pointer again and proceed to the next iteration.

Labuladong Algo Notes provides a more detailed explanation with a template.

Solution

class Solution:
    def minSubArrayLen(self, target: int, nums: List[int]) -> int:
        slow, fast = 0, 0
        sub_sum = 0
        res_len = len(nums) + 1

        while fast < len(nums):

            sub_sum += nums[fast]

            while sub_sum >= target:
                if fast - slow < res_len:
                    res_len = fast - slow + 1
                sub_sum -= nums[slow]
                slow += 1

            fast += 1

        return res_len if res_len <= len(nums) else 0

Relevant Problem Recommendations

Fruit Into Baskets

LeetCode link: 904

class Solution(object):
    def totalFruit(self, fruits):
        """
        :type fruits: List[int]
        :rtype: int
        """
        slow, fast = 0, 0
        basket = dict()
        dict_cnt = 0
        cnt = 0

        while fast < len(fruits):
            if not basket.get(fruits[fast]):
                basket[fruits[fast]] = 1
                dict_cnt += 1
            else:
                basket[fruits[fast]] += 1

            while dict_cnt > 2:
                basket[fruits[slow]] -= 1
                if basket[fruits[slow]] == 0:
                    dict_cnt -= 1
                slow += 1

            if fast - slow + 1 > cnt:
                cnt = fast - slow + 1
            fast += 1
        return cnt

Minimum Window Substring

LeetCode link: 76

class Solution:
    def minWindow(self, s: str, t: str) -> str:
        slow, fast = 0, 0
        t_dict = dict()
        for c in t:
            t_dict[c] = t_dict.get(c,0) + 1
        dict_cnt = len(t_dict)
        res_l = 0
        res_r = 0
        res_len = len(s) + 1

        while fast < len(s):
            if s[fast] in t_dict.keys():
                t_dict[s[fast]] -= 1
                if t_dict[s[fast]] == 0:
                    dict_cnt -= 1
            
            while dict_cnt == 0:
                if fast + 1 - slow < res_len:
                    res_len = fast + 1 - slow
                    res_l = slow
                    res_r = fast + 1

                if s[slow] in t_dict.keys():
                    t_dict[s[slow]] += 1
                    if t_dict[s[slow]] == 1:
                        dict_cnt += 1
                slow += 1
            
            fast += 1
        
        if res_len <= len(s):
            return s[res_l:res_r]
        return ''